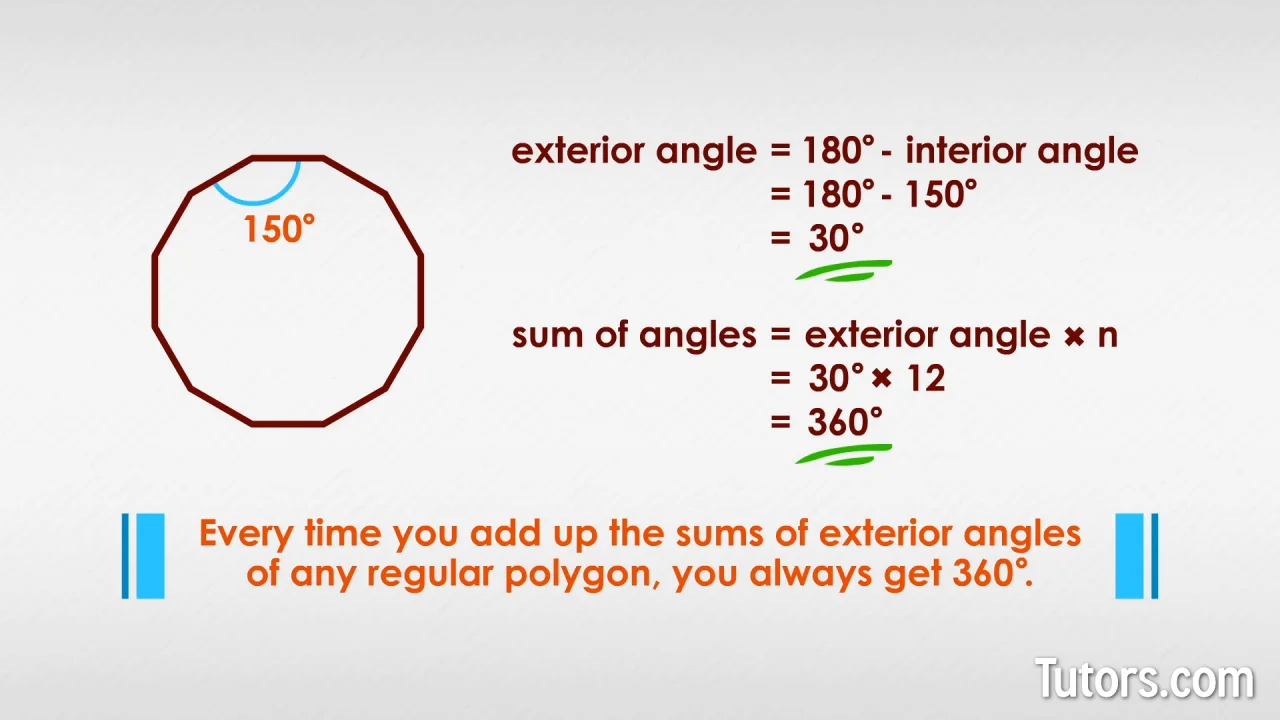
Total Sum Of Interior Angles Of A Polygon

If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360. Exterior angles sum of polygons. An exterior angle of a polygon is made by extending only one of its sides in the outward direction.

small house interior design plans painting house interior cost new york public library interior ministry of interior iqama check interior designers buffalo ny beautiful small house interiors interior cabin doors what is the interior department

$The Sum Of The Interior Angles In A Polygon$

The Sum Of The Interior Angles In A Polygon

Investigate Polygon Interior Angle Sum Geogebra

Gmat Geometry Shortcut For Finding Sum Of Angles Of Polygon

Sum Of Interior Exterior Angles Polygons Pentagon Tutors Com

Sum Of Interior Angles Of An N Sided Polygon Youtube

Video Sum Of The Interior Angles Of A Polygon Nagwa

Check here for more practice.

Total sum of interior angles of a polygon. If it is a regular polygon all sides are equal all angles are equal shape sides sum of interior angles shape each angle. To determine the total sum of the interior angles you need to multiply the number of triangles that form the shape by 180. The sum of interior angles one way to find the sum of the interior angles of a polygon is to divide the polygon into triangles.

Sum of interior angles p 2 180. So we can use this pattern to find the sum of interior angle degrees for even 1 000 sided polygons. Sum of interior angles n 2 180 s u m o f i n t e r i o r a n g l e s n 2 180.

N n 2 180 n 2 180 n. S n 2 180 this is the angle sum of interior angles of a polygon. The sum of the measures of the interior angles of a polygon with n sides is n 2 180.

Here is the formula. Sum of interior angles formula. Let n n equal the number of sides of whatever regular polygon you are studying.

The measure of each interior angle of an equiangular n gon is. In a regular polygon all the interior angles measure the same and hence can be obtained by dividing the sum of the interior angles by the number of sides. The number of triangles is always two less than the number of sides.

Choose one vertex or corner of the polygon and draw straight lines. This gives us the formula total interior angles n 2 180 where n is the number of sides. A heptagon has 7 sides so we take the hexagon s sum of interior angles and add 180 to it getting us 720 180 900 degrees.